I recently finished Andrew Ng’s CS229 course remotely. The course was extremely challenging and covered a wide range of Machine Learning concepts. Even if you have worked with, and used Machine Learning algorithms, he introduced concepts in novel and interesting ways I didn’t expect. One of the things that struct a chord with me was how we worked on K-Means clustering.
The algorithm is quite simple. Courtesy of CS229…
Given a training set, if we want to group it into n clusters
![]()
1. Initialize cluster centroids randomly
![]()
2. Repeat until convergence
For every i set
![]()
For each j set
![]()
Here an example of running K-means on the Iris dataset.
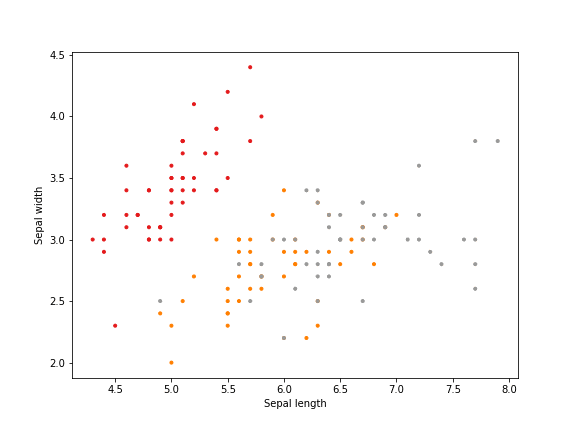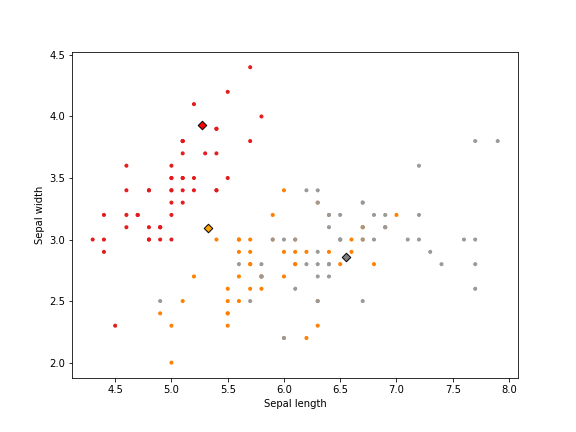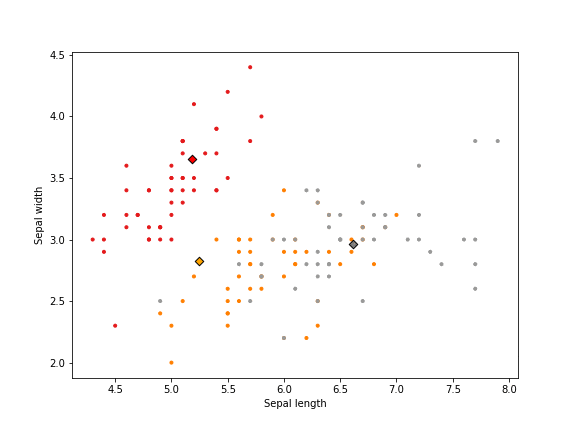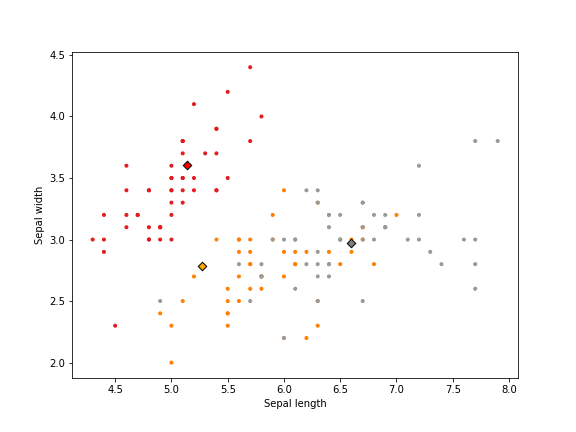
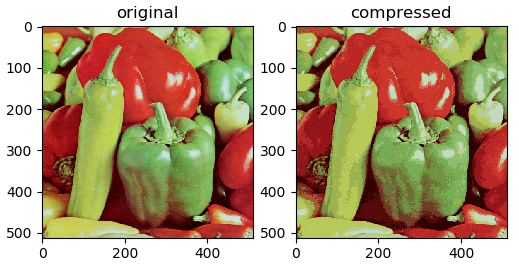
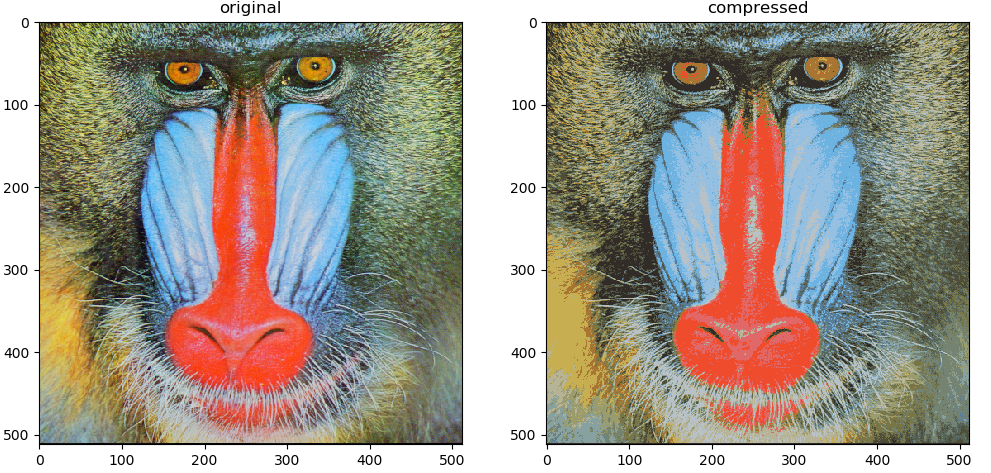
But an alternate use for K-Means is image compression. Given an image with the standard RGB colors we have 256x256x256=16.77M colors. We can use K-Means to compress these into less colors. The idea is similar to the above, with a few differences.
- We take an image of dimension (m,n,3) (3=R,G,B) and resize it to (mxn,3)
- For k clusters, we randomly sample k points from this data
- We assign colors closest to the k points we’ve selected to that cluster
- The new cluster points are the mean R,G,B points for each cluster
- We repeat this process until convergence (points don’t change, or we reach a threshold)
This is what the code looks like
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
def k_means_code(X,num_clusters): min_iters=30 X_reshaped=X.reshape(-1,3) #this variable will get resized past_min_indices =np.zeros(X_reshaped.shape[0]) # first set centroids to random points initial_indices=np.random.choice(X_reshaped.shape[0],num_clusters, replace=False) centroids=X_reshaped[initial_indices] #convert to float to prevent rounding on the averages centroids=centroids.astype(float) i=1 bContinueRunning=True while bContinueRunning: distances=np.array((0,0)) for centroid_index,centroid in enumerate(centroids): distance=np.sqrt(np.sum((X_reshaped - centroid) ** 2, axis=1)) if centroid_index==0: distances=distance.copy() else: distances=np.vstack((distances,distance)) min_indices=distances.argmin(axis=0) if np.sum(min_indices-past_min_indices)==0: bContinueRunning=False else: past_min_indices=min_indices.copy() for centroid_index in range(num_clusters): x_indices_in_centroid = np.where(min_indices == centroid_index)[0] X_in_centroid = X_reshaped[x_indices_in_centroid] centroids[centroid_index] = X_in_centroid.mean(axis=0) i+=1 if i>min_iters: print("Exceeded 30") bContinueRunning=False return centroids |
We can run this on a few images, reducing them from 16.77m colors to 16 colors to see how good the compression is