In the previous post we discussed using Convolutional Neural Networks for Image Recognition. In order to better understand what the algorithms are doing we need to explore convolutions in more detail.
Definition
A convolution of f and g, denoted f*g, is the integral of the product of 2 functions after one is reversed and shifted. Mathematically
![]()
One way of thinking about convolutions is an integral that expresses the amount of overlap of g as it is shifted over f. It “blends” one function with another. The below image courtesy of Wikipedia demonstrates this.
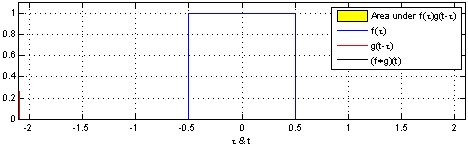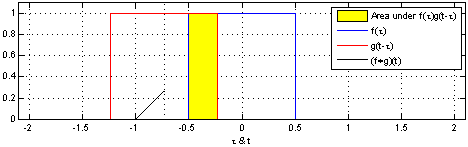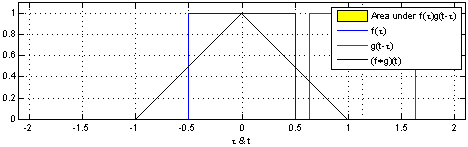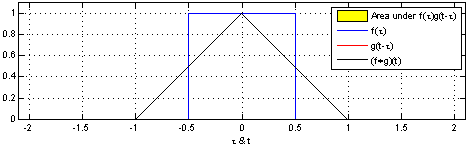 Some more intuitive explanations of convolutions (and more applicable to machine learning):
Some more intuitive explanations of convolutions (and more applicable to machine learning):
Think about a time series. Say we look at the fed funds rate over time. One way to smooth data is to convolve it against a smaller list. For example, to calculate the weekly moving average we convolve it against [1,1,1,1,1]. For a monthly moving average we would convolve it with a list of 25 ones (assuming 25 business days in a month).
One way to smooth data is to convolve it against a smaller list. For example, to calculate the weekly moving average we convolve it against [1,1,1,1,1]. For a monthly moving average we would convolve it with a list of 25 ones (assuming 25 business days in a month).
As another example, consider rolling 2 six sided dice. The probability distribution looks as follows.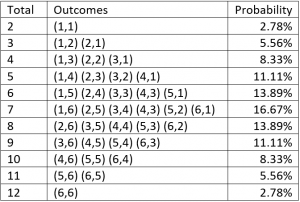 This can be represented as a convolution… For example to get a 4 we have
This can be represented as a convolution… For example to get a 4 we have
So what does the “Convolution” in Convolutional Neural Networks (aka Deep Learning) do to images? Convolutions (called Kernels in image processing) work as feature detectors. Lets look at a few convolutions on 2 images below.
| Convolution | Matrix | Image 1 | Image 2 |
| Original Image |  |
 |
|
| Average | 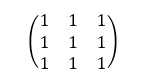 |
 |
 |
| Sharpen | 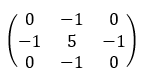 |
 |
 |
| Edge Detection 1 |  |
 |
 |
| Edge Detection 2 |  |
 |
 |
| Edge Detection 3 | 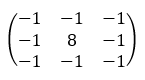 |
 |
 |
| Edge Detection 4 |  |
 |
 |
| Box Blur | 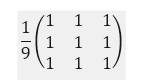 |
 |
 |
| Gaussian Blur | 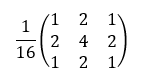 |
 |
 |
| Gradient Detection 1 | 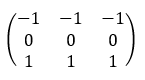 |
 |
 |
| Gradient Detection 2 |  |
 |
 |
The amazing part about Deep Learning is we don’t have to teach the algorithm the convolutions to use. It learns them as part of the hyperparameter tuning!